Accurate Umbral Shadows are Tricky Business ~ 2015-03-17

Note: This post details umbral shadow modeling on EclipseTracks.org. For a larger compositional overview of the EclipseTracks application please see my guest post on the Cesium blog.

Over the past few weeks I've been putting the finishing touches on EclipseTracks.org (version 1.0). This Friday (March 20th, 2015) there will be total solar eclipse that cuts through the Norwegian Sea, casting the Faroe Islands and Svalbard in shadow before running across the north pole. Surely Santa will be outside the workshop sporting his eclipse glasses.

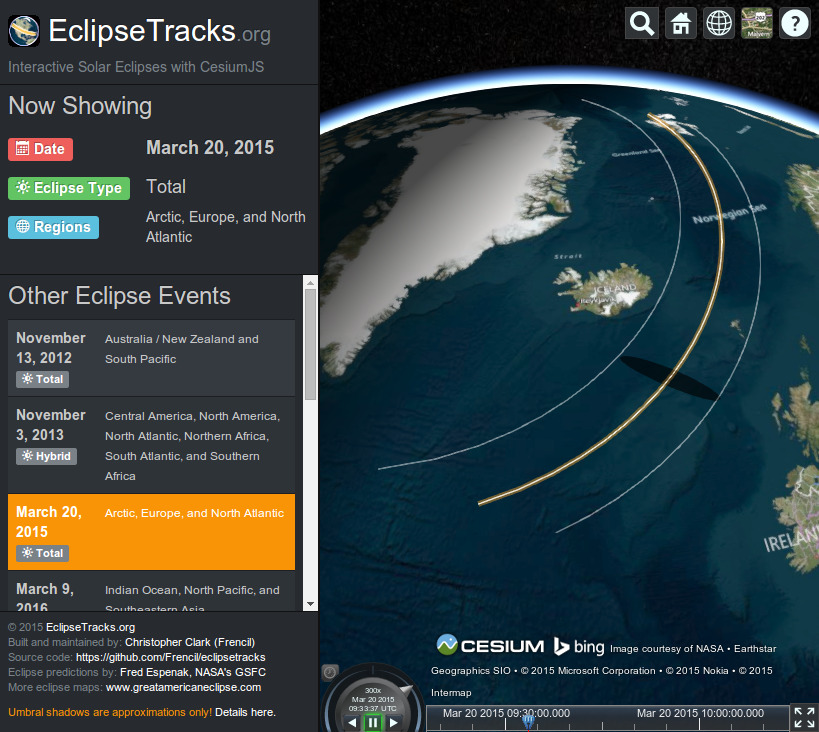
Building EclipseTracks.org has been a tremendous learning experience for a variety of different things. As noted in a disclaimer on the site, though, umbral shadows are approximations only! The umbral shadow is the area where the sun is completely eclipsed by the moon on the surface of the Earth at a given point in time (the penumbral shadow, not currently modeled, is any area where the sun is partially eclipsed). Why?

For starters, the Earth is not a perfect sphere. It's an oblate ellipsoid that's fatter around the equator than pole-to-pole and has some pretty large lumps. In 1984 the world geodetic community developed WGS-84, a set of parameters to define an ellipsoid that more closely matches the actual shape of the Earth. This ellipsoid is still the standard in use today by geodetic systems of all scales, including GPS.

Considering Earth's imperfect shape, how does one accurately predict where an eclipse shadow will fall? The ray-casting geometry involved is comparatively simple when working with spheres but the nuances of where shadows fall with actual ellipsoids in play make this task pretty difficult. Almost 200 years ago a German mathematician and astronomer named Friedrich Wilhelm Bessel devised a more direct approach. Instead of trying to figure out how the shadow is cast on the ellipsoid surface he created a plane through the ellipsoid perpendicular to a line drawn between the center of the moon and the center of the Earth (the shadow axis). On this plane the shadow is a much more friendly circle, and its movements during an eclipse event can be described with only a few numbers. These numbers are today referred to as Besselian elements.

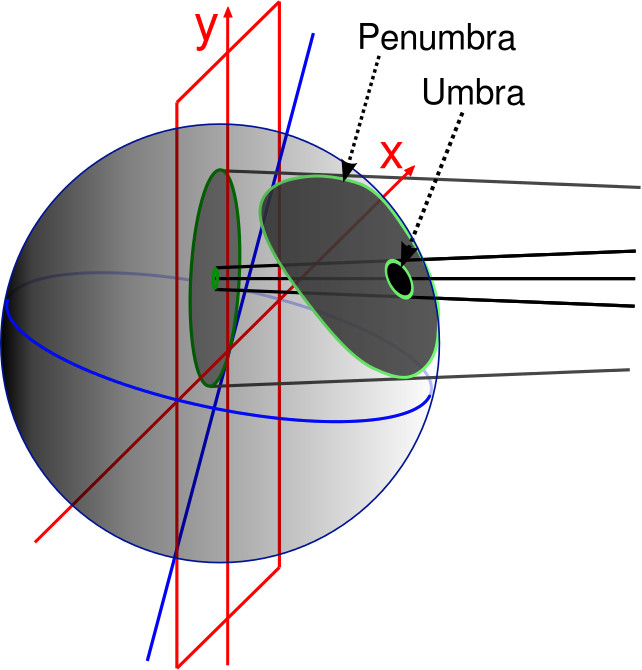
Once Besselian elements are used to generate the movements of the umbral and penumbral shadows in the plane, along with the accompanying shadow cone, any model of the Earth can be applied. As in the figure above, one could use the current standard WGS-84 model of the Earth and find the intersections of the shadow cone with the surface at arbitrary times during an eclipse event to trace the path and shape of the umbral and penumbral shadows to a very high degree of accuracy.

EclipseTracks.org doesn't go this far (yet). Instead the paths for the northern/southern umbral shadow limits and central track of any given eclipse are defined using tables provided by NASA. These tables were generated using the method described immediately above with the Besselian elements for the eclipse in question.

While scraping NASA's derived tabular data to draw some polylines in Cesium is relatively way easier than modeling a Besselian shadow cone's intersection with the surface of the WGS-84 ellipsoid I still wanted some approximation of the umbral shadow for a proof of concept. The method EclipseTracks.org uses presently involves defining a shadow ellipse for every defined point in the event (these are usually spaced two minutes apart and defined by a central track point, a northern umbral limit, and southern umbral limit, along with various other details like sun altitude and azimuth). Cesium does a good job of interpolating shapes defined on intervals this way. Here's the general procedure in play right now for approximating the umbral shadow at each point in time:

1. Position the center of the ellipse on the central track position at time t.
2. Approximate ellipse semi-major axis by taking Vincenty distance (on a WGS-84 ellipsoid) between northern and southern umbral limits at time t.
3. Approximate ellipse semi-minor axis using the sun's altitude at time t in reference to the semi-major axis (near equal when the sun is overhead, smaller when the sun is near the horizon).*
4. Approximate ellipse rotation by averaging the initial and final bearings between the northern and southern umbral limits at time t**.

* This is an arbitrary method chosen to make the shadows look "close enough" for the upcoming March 20, 2015 event. It's not even close to correct!

** This bearing is calculated on a spheroid, not a WGS-84 due to conflicts in versions for available Python modules. Also, bearing with respect to polar north typically changes as you move along an ellipsoid/spheroid so an average of initial and final bearing (initial being north-to-south and final being south-to-north, inverted) was the closest approximation available.

Source code for the above steps can be seen here (in the czml() method).

All of these gymnastics, complicated in their own way, get a reasonable approximation for a proof-of-concept of an umbral shadow. Obviously this entire approach is fundamentally flawed as I'm trying to draw a two dimensional shape (an ellipse) onto a three dimensional ellipsoid. Umbral shadows for eclipses can be pretty big—hundreds of kilometers across—so the curvature of the Earth is something that can't just be smoothed away.

So, lesson learned: accurate umbral shadows are tricky business! At any rate EclipseTracks.org is live with those "good enough for now" approximations of umbral shadows with much more accurate track polylines. After this Friday's solar eclipse we've got two lined up in 2016: March 9th that stretches across Indonesia and the South Pacific and September 1st that stretches across southern Africa and the Indian Ocean.

The big one for folks in my corner of the world isn't until August 21st, 2017. That's the one that set off this project in the first place, as I know I'll be camping in some wilderness along that track somewhere but just don't know quite where just yet. Maybe by then I'll have proper shadow rendering with Besselian elements, and then I can use EclipseTracks.org to find the best camping spot in the country.

In the meantime I would be very happy for feedback and contributions on the eclipsescraper python module, the eclipsetracks source code, or EclipseTracks.org itself!